Kettősréteg

https://www.plasma-universe.com/Double_layer

A kettősréteg a plazmában kialakuló struktúra, két ellentétes töltésű, párhuzamos rétegből áll. A töltött fegyverzetek erős elektromos teret hoznak létre, ennek következtében éles változás következik be az elektromos potenciálban a kettősrétegen keresztül. A kettősrétegbe belépő ionokat és elektronokat az elektromos mező felgyorsítja, lassítja vagy akár vissza is fordíthatja. Általában a kettős rétegek (amelyek szinte mindig görbültek és nem laposak, mint a laboratóriumi üvegcsőben) választják el a plazma nagyon különböző jellemzőjű területeit. A kettősrétegek megtalálhatók különböző plazmákban a kisülési csövektől az űrplazmákig, a Föld Auroráját fenntartó Birkeland-áramokig és különösen gyakran fordulnak elő az áram vezető plazmákban. A kettősréteget tartalmazó plazmák méretéhez viszonyítva a maguk a kettősrétegek nagyon vékonyak (jellemzően tíz Debye-hosszúságúak), szélességük a laboratóriumi plazmák néhány milliméterétől az asztrofizikai plazmák több ezer kilométeréig terjed.

A kettős réteg más elnevezései: elektrosztatikus kettősréteg, elektromos kettősréteg, plazma kettősréteg, elektrosztatikus sokk (olyan típusú kettősréteg, amely ferde szöget zár be a mágneses mezővel úgy, hogy a merőleges elektromos mező jóval nagyobb, mint a párhuzamos elektromos mező), [6] kozmikus töltött réteg, [7] és "potencia rámpa". [8] Lézerfizikában a kettős réteget néha ambipoláris elektromos mezőnek nevezik [9]. A kettős rétegek fogalmilag kapcsolódnak a „köpeny” és a „burok” fogalmához (lásd Debye burok).

Az elektromos áramkörben lévő kettősréteg (Double Layer) elfogadott elektromos szimbóluma:
────DL────
Ha van nettó áram, akkor a DL-t úgy kell igazítani, hogy az L betű alapja összhangban legyen áram irányával. [10]

A Világűrben található kettősrétegekről, kísérletekről és szimulációról Ph.D Thesis [11] írásában olvashatunk.

1. A kettősrétegek osztályozása

A kettősrétegeket a következőképpen csoportosíthatjuk:

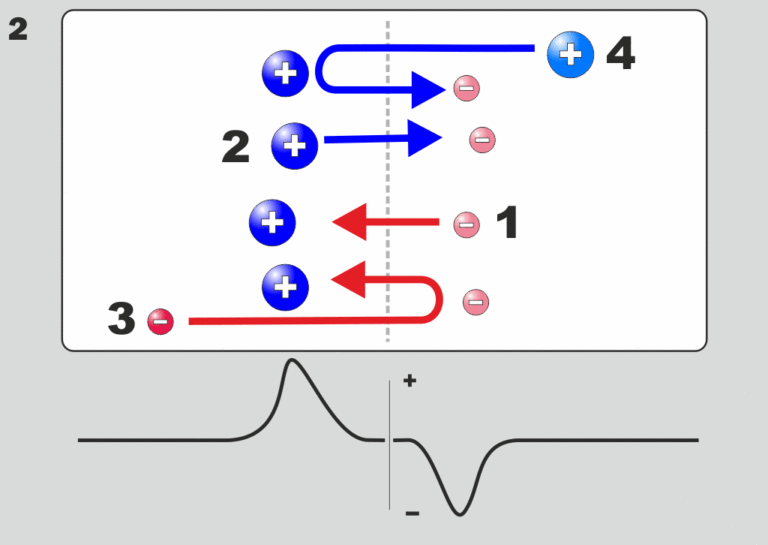
• Gyenge és erős kettősrétegek. A kettősréteg erősségét a plazma potenciálcsökkenésének aránya fejezi ki a plazma ekvivalens hőpotenciájához vagy az elektronok nyugalmi tömeg energiájához képest. Akkor mondjuk a kettős rétegről, hogy erős, ha az elektromos potenciálesés a rétegen nagyobb, mint a plazma alkotóelemeinek ekvivalens hőpotenciálja. Ez azt jelenti, hogy az erős kettősrétegek a plazmában négy különféle módon viselkedhetnek:
  • azok az elektronok(-), amelyek a kettősréteg alacsony potenciálú oldalán lépnek be, gyorsulnak;
  • azok az ionok(+), amelyek a kettősréteg magas potenciálú oldala felől lépnek be, gyorsulnak;
  • a kettősréteg magas potenciáljának oldalán belépő elektronok(-) lelassulnak és rendre visszaverődnek;
  • azon ionok(+), amelyek az alacsony potenciálú oldalon lépnek be a kettősrétegbe, lelassulnak és visszaverődnek.
    (Vegyük figyelembe, hogy gyenge kettőséteg esetén a „rossz” oldalról érkező elektronokat és ionokat az elektromos mező lassítja, ám a legtöbb nem verődik vissza, mivel a potenciálesés nem elég erős.)
• Relativisztikus vagy nem relativisztikus kettős rétegek. Egy kettősréteg akkor a relativisztikus, ha a feszültségesés a rétegben olyan nagy, hogy a részecske által elnyelt teljes energiamennyiség nagyobb, mint az elektron nyugalmi tömege. A töltés eloszlása egy relativisztikus kettőstegben olyan, hogy a töltéssűrűség két nagyon vékony rétegben található, és a rétegek között a töltéssűrűség konstans és nagyon alacsony a plazma többi részéhez képest. Ebben a tekintetben a kettősréteg töltéseloszlása hasonló egy kondenzátor töltéseloszlásához. A relativisztikus kettősrétegek speciális esete a pulzárok mágneses sarki sapkáján található vákuum rés.
• Áram hordozó és árammentes kettős rétegek is előfordulhatnak. Áram hordozó kettősrétegeket hozhatnak létre áram-vezérelt plazma instabilitások, amelyek felerősítik a különféle sűrűségű plazmákat. Árammentes kettős rétegek alakulhatnak ki eltérő jellemzőkkel rendelkező két plazma régió közötti felületen. A hozzájuk kapcsolódó elektromos mező egyensúlyt tart fenn az elektronok bármely irányba történő áthatolásával szemben (, így a nettó áram alacsony marad).

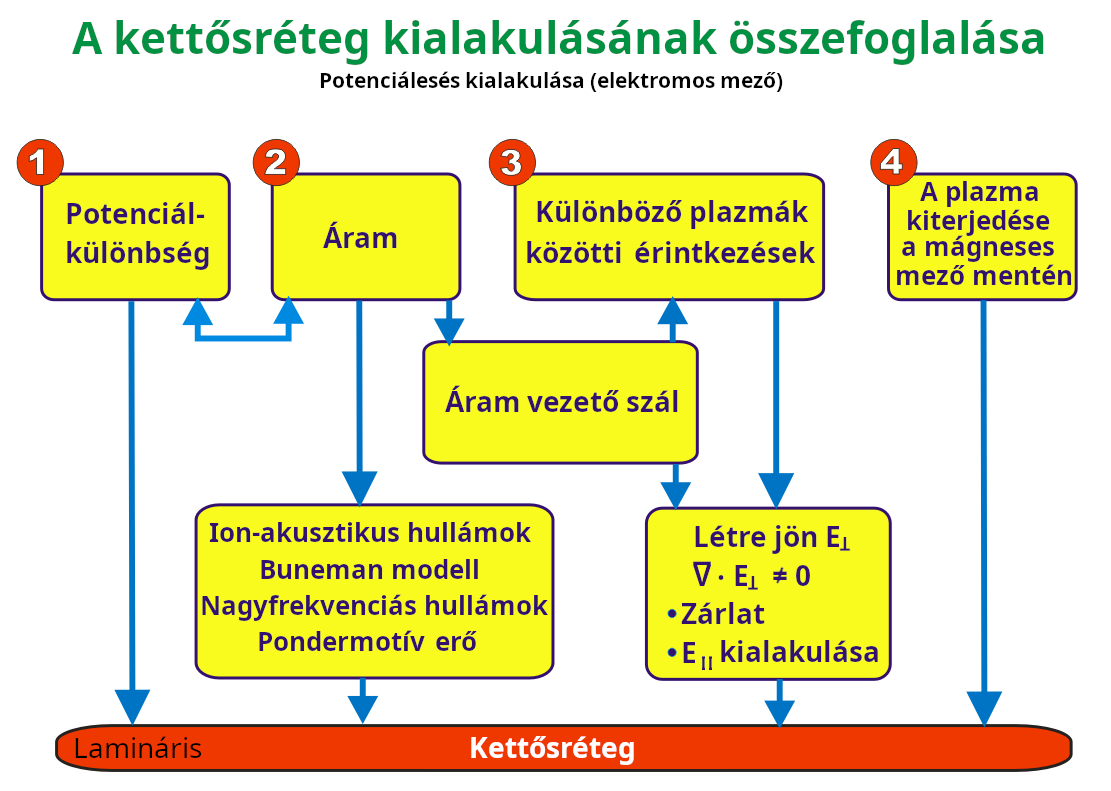
2. Kettősrétegek kialakulása

 

Kétféle kettős réteg létezik, amelyek eltérő módon alakulnak ki:

Áram hordozó kettős rétegek

Áram hordozó kettősrétegek olyan plazmákban alakulhatnak ki, amelyeken áram folyik keresztül. Különféle instabilitások lehetnek felelősek az ilyen rétegek kialakulásáért. Példa erre a Buneman instabilitás, amely akkor fordul elő, amikor az elektronok áramlási sebessége (alapvetően az áramsűrűség elosztva az elektronsűrűséggel) meghaladja a plazma elektron hőmérsékleti sebességét. Az instabilitás nemlineáris fázisában gyakran kettősrétegek (és más fázisú űr-struktúrák) alakulnak ki. A Buneman instabilitás megfigyelésének egyik módja annak leírása, hogy mi történik, amikor az áramnak (nulla hőmérsékletű elektronnyaláb formájában) át kell haladnia egy csökkent ionsűrűségű tartományon. A töltés felhalmozódásának elkerülése érdekében a rendszerben az áramnak mindenütt azonosnak kell lennie (ebben az 1D modellben). Az elektron sűrűségnek is hasonlónak lennie az ion sűrűségéhez (kvázineutralitás) - tehát az elektron sűrűség alacsony. Az elektronokat ezért fel kell gyorsítani, hogy megmaradjon az áramsűrűség a töltéshordozók alacsonyabb sűrűsége mellett, amelyhez magas elektromos potenciálkülönbség szükséges. Ennek következményeként az ionok felgyorsulnak a rétegen át, felerősítve a sűrű és ritkább plazma perturbációját. A kialakult kettős-kettősréteg egyik oldalát a plazma valószínűleg eltávolítja (konvekció), így normál kettős réteg marad. Ez az a folyamat, amely során kettősrétegeket alakulnak ki egy bolygó magnetoszférájában az úgynevezett Birkeland-áramokban.

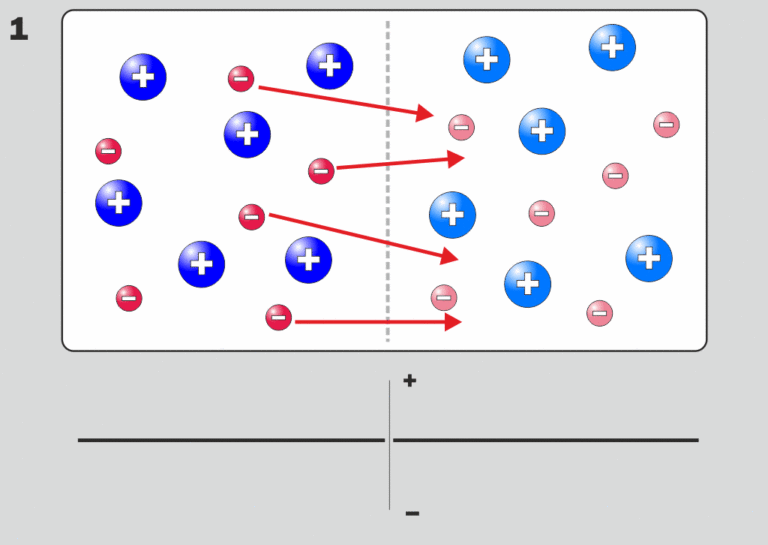
Árammnetes kettősrétegek

Az árammentes kettős rétegek a különböző plazma tulajdonságokkal rendelkező plazma régiók közötti határokon fordulnak elő. A következőképpen alakulhatnak ki (figyelmen kívül hagyva az ionokat, amelyeket kizárólag semlegesítő háttérnek tekintünk). Vegyük egy síkkal két régióra osztott plazmát, amelynek egyik oldalán az elektron hőmérséklete magasabb, mint a másik oldalán (ugyanez a gondolatkísérlet különböző sűrűségekre is elvégezhető). Ez azt jelenti, hogy a rendszer egyik oldalán lévő elektronok nagyobb hősebességgel rendelkeznek. Az elektronok bármelyik irányba szabadon áramolhatnak. Az elektronok fluxusa a forró plazmától a hideg plazmáig nagyobb lesz, mint az elektronok fluxusa a hideg plazmától a forró plazmáig, mivel a forró oldalról származó elektronoknak nagyobb az átlagsebessége. Mivel sokkal több elektron lép be a hideg plazmába, mint amennyi kilép, a hideg régió egy része negatív töltésűvé válik. A forró plazma viszont pozitív töltésű lesz. Ezért elektromos mező jön létre, amely az elektronokat felgyorsítja a forró régió felé, csökkentve a nettó fluxust. Az elektromos mező csak addig marad fenn, amíg az elektronok fluxusai valamelyik irányban nem egyenlők, és megakadályozzuk a további töltés felhalmozódását a két plazmában. A feszültségesés valójában pontosan megegyezik a két plazma régió közötti hőpotenciál különbséggel, tehát egy ilyen kettősréteg ritkán tekinthető erős kettősrétegnek.

Double layer formation mechanisms

The Moon. The prediction of a lunar double layer[14] was confirmed in 2003[15] . In the shadows, the Moon charges negatively in the interplanetary medium.[16] and when the Moon passes through the Earth's Magnetotail.[17]

The details of the formation mechanism depend on the environment of the plasma (eg. double layers in the laboratory, ionosphere, space plasmas, fusions plasma, etc). Proposed mechanisms for their formation have included:

    1971: Between plasmas of different temperatures[18]
    1976: In laboratory plasmas[19]
    1982: Disruption of a neutral current sheet[20]
    1983: Injection of non-neutral electron current into a cold plasma[21]
    1985: Increasing the current density in a plasma[22]
    1986: In the accretion column of a neutron star[23]
    1986: By pinches in cosmic plasma regions [24]
    1987: In a plasma constrained by a magnetic mirror[25]
    1988: By an electrical discharge[26]
    1988: Current-driven instabilities (strong double layers)[27]
    1988: Spacecraft-ejected electron beams[28]
    1989: From shock waves in a plasma[29]
    2000: Laser radiation[30]
    2002: When magnetic field-aligned currents encounter density cavities[31]
    2003: By the incidence of plasma on the dark side of the Moon's surface[32]

Features and characteristics of double layers

Double layer characteristics showing the potential (Φ), electric field (E) and space charge distribution (ρ) across the layer

    Thickness: The production of a double layer requires regions with a significant excess of positive or negative charge, that is, where quasi-neutrality is violated.[33][34] In general, quasi-neutrality can only be violated on scales of the order of the Debye length. The thickness of a double layer is of the order of ten Debye lengths, which is a few centimeters in the ionosphere, a few tens of meters in the interplanetary medium, and tens of kilometers in the intergalactic medium.
    Particle acceleration: The potential drop across the double layer will accelerate electrons and positive ions in opposite directions. The magnitude of the potential drop determines the acceleration of the charged particles. In strong double layers, this will result in beams or jets of charged particles.
    Particle populations: As described in the formation of double layers, there are four populations of charge particles inside a double layer (1) Free electrons that are accelerated across the double layer (2) Free positive ions that are accelerated in the opposite direction across the double layer (3) Reflected electrons that approach the double layer, but are reflected back and counter stream away (4) Reflected positive ions that approach the double layer, but are reflected back and counter stream away. Note that in the case of weak double layers not all electrons and ions entering "from the wrong side" will be reflected, and therefore there will also be a population of decelerated electrons and ions.

    Particle flux: For non-relativistic current carrying double layers the electrons comprise the main part of the particle flux. The Langmuir condition states that the ratio of the electron and the ion current across the layer is given by the square root of the mass ratio of the ions to the electrons.[35] For relativistic double layers the current ratio is 1, i.e. equal amounts of current are carried by the electrons and the ions.
    Energy supply: In a certain limit, the voltage drop across a current-carrying double layer is proportional to the total current, and it might be thought of as a resistive element (or load) which absorbs energy in an electric circuit. Anthony Peratt (1991) wrote: "Since the double layer acts as a load, there has to be an external source maintaining the potential difference and driving the current. In the laboratory this source is usually an electrical power supply, whereas in space it may be the magnetic energy stored in an extended current system, which responds to a change in current with an inductive voltage".[36]
    Stability: Double layers in laboratory plasmas may be stable or unstable depending on the parameter regime.[37] Various types of instabilities may occur, often arising due to the formation of beams of ions and electrons. Unstable double layers are noisy in the sense that they produce oscillations across a wide frequency band. A lack of plasma stability may also lead to a dramatic change in configuration often referred to as an explosion (and hence exploding double layer). In one example, the region enclosed in the double layer rapidly expands and evolves.[38] An explosion of this type was first discovered in mercury rectifiers used in high-power direct-current transmission lines, where the voltage drop across the device was seen to increase by several orders of magnitude. Double layers may also drift, usually in the direction of the emitted electron beam, and in this respect are natural analogues to the smooth bore magnetron.[39]) (not to be confused with a unit of magnetic moment, the Bohr magnetron, which is created by the "classical circular motion" of an electron around a proton).

Location    Typical
Voltage drop    Source
Ionosphere    102- 104V    Satellite
Solar    109- 1011V    Estimated[40]
Neutron star    1015V    Estimated[41]
Galactic filament    1017V    Estimated[36]
Typical Double Layers

    Magnetised plasmas: Double layers can both form in unmagnetised and magnetised plasmas.
    Cellular nature: While double layers are relatively thin, they will spread over the entire cross surface of a laboratory container. Likewise where adjacent plasma regions have different properties, double layers will form and tend to cellularise the different regions.[42]
    Energy transfer: Double layers fascilitate the transfer of electrical energy into kinetic energy, dW/dt=I.ΔV where I is the electric current dissipating energy into a double layer with a voltage drop of ΔV. Alfvén points out that the current may well consist exclusively of low-energy particles.[43] Torvén et al. also report that plasma may spontaneously transfer magnetically stored energy into kinetic energy by electric double layers.[44]
    Oblique double layer: An oblique double layer has its electric field not parallel to the background magnetic field (i.e. it is not field-aligned).
    Simulation: Double layers may be modelled using kinetic computer models like particle-in-cell (PIC) simulations. In some cases it is reasonable to treat the plasma as essentially one- or two-dimensional to reduce the computational cost of a simulation.
    Bohm Criterion: A double layer cannot exist under all circumstances. In order to achieve that the electric field vanishes at the boundaries of the double layer, an existence criterion says that there is a maximum to the temperature of the ambient plasma. This is the so-called Bohm criterion.[45] (A mathematical description is given in the math section)
    Bio-physical analogy: A model of plasma double layers has been used to investigate their applicability to understanding ion transport across biological cell membranes.[46] Brazilian researchers have note that "Concepts like charge neutrality, Debye length, and double layer are very useful to explain the electrical properties of a cellular membrane.".[47] Plasma physicist Hannes Alfvén also noted that association of double layers with cellular structure,[48] as had Irving Langmuir before him, who coined the named "plasma" after its resemblance to blood cells.[49]

History of double layers

File:Alfven-wave-double-layer.gif
A cluster of double layers forming in an Alfvén wave, about a sixth of the distance from the left. Click for more details

The research of these objects is a relatively young phenomenon. Although it was already known in the 1920s that a plasma has a limited capacity for current maintenance Irving Langmuir.[50] He characterized double layers in the laboratory and called these structures double-sheaths. It was not until the 1950s that a thorough study of double layers started in the laboratory (e.g. Schönhuber, 1958)[Citation needed]. At the moment many groups are working on this topic theoretically, experimentally and numerically. It was first proposed by Hannes Alfvén (the developer of magnetohydrodynamics) that the creation of the polar lights or Aurora Borealis is created by accelerated electrons in the magnetosphere of the Earth.[51] He supposed that the electrons were accelerated electrostatically by an electric field localized in a small volume bounded by two charged regions. This so-called double layer would accelerate electrons Earthwards. Many experiments with rockets and satellites have been performed to investigate the magnetosphere and acceleration regions. The first indication for the existence of electric field aligned along the magnetic field (or double layers) in the magnetosphere was by a rocket experiment by McIlwain (1960). Later, in 1977, Forrest Mozer reported that satellites had detected the signature of double layers (which he called electrostatic shocks) in the magnetosphere.[52]

The most definite proof of these structures was obtained by the Viking satellite,[53] which measures the differential potential structures in the magnetosphere with probes mounted on 40 m long booms. These probes can measure the local particle density and the potential difference between two points 80m apart. Asymmetric potential structures with respect to 0 V were measured, which means that the structure has a net potential and can be regarded as a double layer. The particle densities measured in such structures can be a los as 33% of the background density. The structures usually have an extent of 100 m (a few tens of Debye lengths). The filling factor of the lower magnetosphere with such solitary structures is about 10%. If one out of 5 such structures has a net potential drop of 1 V then the total potential drop over a region of 5000 km would be more than the 1 kV which is needed for the electrons to create the aurora. Magnetospheric double layers typically have a strength
eϕDL/kBTe≈0.1

(where the electron temperature is assumed to lie in the range (
2eV≤kBTe≤20eV

) and are therefore weak. In the laboratory double layers can be created in different devices. The are investigated in double plasma machines, triple plasma machines and Q-machines. The stationary potential structures which can be measured in these machines agree very well with what one would expect theoretically. An example of a laboratory double layer can be seen in the figure below, taken from Torvén and Linberg (1980), where we can see how well-defined and confined the potential drop of a double layer in a double plasma machine is. On of the interesting things of the experiment by Torvén and Lindberg (1980)[54] is that not only did the measure the potential structure in the double plasma machine but they also found high-frequency fluctuating electric fields at the high-potential side of the double layer (also shown in the figure). These fluctuations are probably due to a beam-plasma interaction outside the double layer which excites plasma turbulence. Their observations are consistent with experiments on electromagnetic radiation emitted by double layers in a double plasma machine by Volwerk (1993),[55] who, however, also observed radiation from the double layer itself. The power of these fluctuations has a maximum around the plasma frequency of the ambient plasma.

A recent development in double layer experiments is the investigation of so-called stairstep double layers. It has been observed that a potential drop in a plasma column can be split up into different parts. Transitions from a single double layer into two, three or more-step double layers are strongly sensitive to the boundary conditions of the plasma (Hershkowitz, 1992)[Citation needed]. These experiments can give us information about the formation of the magnetospheric double layers and their possible role in creating the aurora.

Some scientists have subsequently suggested a role of double layers in solar flares[56][57][58]
Mathematical description of a double layer.

In this section we will take a closer look at the mathematics behind double layers. We first describe a semi-quantitative criterion for the formation of a density dip. We then describe a particularly simple kind of double layer. We then explain how to use the distribution function and the Vlasov-Poisson equation to model more complex double layers.
Formation of a density dip.

First we will take a look at the generation of a double layer in a current carrying plasma. In 1968 Alfvén and Carlqvist showed that a density dip in a current carrying plasma can be favourable for the generation of a double layer. In this case we look at the plasma as a combination of two fluids, the moving electron fluid and the immobile ion fluid which acts as a neutralizing background. The electron fluid is treated as an essentially zero temperature beam and the ions are assumed to be collisional, and possess some finite temperature. The density dip in the plasma (of both electrons and ions) will cause an electric field to be generated in order to keep the current density at the same level, i.e. electrons are accelerated in the decreasing part into the dip and decelerated in the increasing part out of the dip. However, this electric field will also have an influence on the first as immobile assumed ions. These ions will be driven out of the density dip, increasing it, and thereby increasing the electric field. When all ions are gone, the electric field has reached its maximum value over the dip. Note that we then have a double-double layer (increasing and decreasing electric field), and one side needs to be transported away.

We will use the quasi-static, non-relativistic description of this mechanism, which is governed by the continuity equation and the momentum equation:

∂∂x(neve)=0

 

meve>∂ve∂x=−eE

 

Combining these two equations we get an expression for the electric field dependent on the electron density:
E=−∂∂x(mej2e2n2ee3)

where
je=−neeve

the electron current density. The ions will experience an outward force due to this electric field, with
F=eniE=−∂∂x(menev2e)

. Only when the force of the electric field can overcome the force by the ion pressure gradient can the evacuation of the density dip take place. Comparing the two forces (pressure and electric) assuming a quasi-neutral, thermal plasma shows after integration that this can only happen when
kBTi<mev2e

. This happens to be the Bohm criterion for the stability of a double layer (more below).
Current carrying double layers formed by single, zero temperature beams.

File:Doublelayer.png
The electron (red) and ion (blue) distributions in phase (velocity and position) space for the double layer described in this section. There are two beam-like (zero temperature) components for each species. The ion velocity is not to scale: it is exaggerated for the purposes of visualisation.

We consider how a single zero-temperature beam of ions and a single zero-temperature beam of electrons, together with a trapped, zero velocity ion component, and a trapped, zero velocity electron component, may form a particular class of double layer. The trapped components are referred to as the 'ambient plasma' and will later be allowed to have finite temperature.

We use Poisson's equation and the conservation of momentum and number density to analyse the structure of these double layers, in the 1D, time-independent limit. We are looking for double layer like solutions, where there is a well localised region with a potential gradient, outside of which the electric field is zero. The region can be divided into the interval inside the double layer, where there is only one ion component and one electron component, but there is a finite field, and the outside region, where the electric field is zero. For the moment, we need only consider the inside region and the densities and velocities associated with the beams inside the layer.

The electron beam component is streaming with positive velocity
ve(x)

(to the right), and the ion beam is streaming with negative velocity
vi(x)

(to the left). Here, the conservation of particle energy means that
v2α(x)/2m+qαϕ(x)

is a constant, and the conservation of particle number means that the current
jα=qnα(x)vα(x)

is also a constant.

|vα(ϕα)|=v2α,0+2eϕαmα−−−−−−−−−−√,

 

nα(ϕα)=n0vα,0v−1α(ϕα)

 

where
ϕe=ϕ

and
ϕi=ϕDL−ϕ

. Here
n0

and
vα,0

are respectively the electron (and ion) density and particle drift speed at the low (high) potential side of the double layer.

Now we use Poisson’s equation to obtain the maximal current through the double layer, as a function of the potential drop, the fraction of current carried by the ions as compared to the electrons and a temperature limit for the ambient plasma. We chose
ϕ(x=0)=0

and
ϕ(x=d)=ϕDL

, with
d

the thickness of the double layer.

ρe=jeve,ρi=jivi.

 

Thus we can write Poisson’s equation in the region inside the double layer as:

−14π∂2ϕ∂x2=jiv2i,0+2e(ϕDL−ϕ)/mi−−−−−−−−−−−−−−−−−−√−jev2e,0+2eϕ/me−−−−−−−−−−−√.

 

Introducing an integration factor
dϕ/dx

at both sides and integrating over
x

at the left hand side and over
ϕ

on the right hand side the first integration leads to the square of the electric field
(dϕ/dx)2

. The assumption that there is no electric field outside the double layer then leads to the ‘’Langmuir condition’’ for non-relativistic double layers:

jeji=mime.

 

For this double layer (in a hydrogen plasma) the electron current dominates the ion current by a factor of
1836−−−−√

. (Note that for the same theory for ultra-relativistic double layers gives this fraction equal to 1). Further integration, as done by Raadu (1989), then leads to the Langmuir-Child relation:

jd2=(je+ji)d2=(1+memi−−−√)C092eme−−−√ϕ1.5DL,

 

where
C0

is expressed in terms of the elliptical integrals E and K:

C0=2−1.5(22–√E(sinπ/8)−(1+22–√K(sinπ/8))2≈1.86518.

 

If we now allow the ambient plasma to be at finite temperature we have to take into account reflected particles more carefully and examine how far they can penetrate into the repulsive electric field. We describe the ambient plasma by a Boltzmann distribution over the double layer:

nα,R=nα,0e−eϕαkBTα

 

The densities of the reflected particles are now added to Poisson’s equation. In order that the particles in the 'ambient plasma' be truly trapped we require that their temperature be lower than the double layer potential. This can be seen in terms of the restriction that the potential and the electric field have to vanish at the boundaries of the double layer. The precise condition is known as the ‘’Bohm criterion’’:

mev2e>kBTi.

 

A double layer of this type cannot form if this criterion is not met. This is the same condition under which a double layer can be formed by an ion density dip (or equivalently, for instability to parallel wavemodes like the ion acoustic or Buneman instability) as discussed before.
The Vlasov-Poisson equation.

In general the plasma distributions near a double layer are necessarily strongly non-Maxwellian, and therefore inaccessible to fluid models. In order to analyse double layers in full generality, the plasma must be described using the particle distribution function
fα(x⃗ ,t;v⃗ )

, which describes the number of particles of species
α

having approximately the velocity
v⃗

near the place
x⃗

and time
t

.

The Vlasov-Poisson equations give the time-dependent interaction of a plasma (described using the particle distribution) with its self-consistent electric field. The Vlasov-Poisson equations are a combination of the Vlasov equations for each species
α

(also called the collisionless Boltzmann equation (CBE). We take the nonrelativistic zero-magnetic field limit);

∂∂tfα+v⃗ ⋅∂∂x⃗ fα+qαE⃗ mα⋅∂∂v⃗ fα=0,

 

and Poisson’s equation:

∇⋅E⃗ =−∂2ϕ∂x2=4πρ.

 

Here
qα

is the particle’s electric charge,
mα

is the particle’s mass,
E⃗ (x⃗ ,t)

is the electric field,
ϕ(x⃗ ,t)

the electric potential and
ρ

is the electric charge density.

Hivatkozások

    Astronomy Picture of the Day: 23 December 2001 (NASA)
    Isbell, J.; Dessler, A. J.; Waite, J. H. "Magnetospheric energization by interaction between planetary spin and the solar wind" (1984) Journal of Geophysical Research, Volume 89, Issue A12, p. 10715-10722
    Theisen, William L. "Langmuir Bursts and Filamentary Double Layers in Plasmas." (1994) Ph.D Thesis U. of Iowa, 1994
    Deverapalli, C. M.; Singh, N.; Khazanov, I. "Filamentary Structures in U-Shaped Double Layers" (2005) American Geophysical Union, Fall Meeting 2005, abstract #SM41C-1202
    Borovsky, Joseph E. "Double layers do accelerate particles in the auroral zone" (1992) Physical Review Letters (ISSN 0031-9007), vol. 69, no. 7, Aug. 17, 1992, p. 1054-1056
    Temerin, M.; Mozer, F. S., "Double Layers Above the Aurora" (1987) NASA Conference Publication, #2469 (Record | Full text)
    Block, L. P. "A double layer review" FULL TEXT (1978) Astrophysics and Space Science, vol. 55, no. 1, May 1978, p. 59-83 PEER REVIEWED
    D. L. Newman, M. V. Goldman, R. E. Ergun, and A. Mangeney, "Formation of Double Layers and Electron Holes in a Current-Driven Space Plasma", Phys. Rev. Lett. 87, 255001 (2001)
    Bulgakova, Nadezhda M. et al, "Double layer effects in laser-ablation plasma plumes", Physical Review E (Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics), Volume 62, Issue 4, October 2000, pp.5624-5635
    Double Layers in Astrophysics, NASA Conference Publication 2469 (NASA CP-2469), (1987) Edited by Alton C. Williams and Tauna W. Moorhead (Record | Full text) FULL TEXT
    Meige, A. "Numerical modeling of low-pressure plasmas: applications to electric double layers." Ph.D Thesis, The Australian National University, 2006 FULL TEXT PDF
    See "Helicon Double Layer Thruster study", European Space Agency; "ESA accelerates towards a new space thruster" (2005)
    Singh, Nagendra; Thiemann, H.; Schunk, R. W., "Electric Fields and Double Layers in Plasmas (1987) Double Layers in Astrophysics, Proceedings of a Workshop held in Huntsville, Ala., 17-19 Mar. 1986. Edited by Alton C. Williams and Tauna W. Moorehead. NASA Conference Publication, #2469" (Record | Full text)
    Borisov, N.; Mall, U. "The structure of the double layer behind the Moon" (2002) Journal of Plasma Physics, vol. 67, Issue 04, p.277-299
    Halekas, J. S.; Lin, R. P.; Mitchell, D. L. "Inferring the scale height of the lunar nightside double layer" (2003) Geophysical Research Letters, Volume 30, Issue 21, pp. PLA 1-1. (PDF)
    Halekas, J. S et al "Evidence for negative charging of the lunar surface in shadow" (2002) Geophysical Research Letters, Volume 29, Issue 10, pp. 77-1
    "Moon Gets A Lashing From Earth's Magnetotail" ScienceDaily (Apr. 21, 2008)
    Hultqvist, Bengt, "On the production of a magnetic-field-aligned electric field by the interaction between the hot magnetospheric plasma and the cold ionosphere" (1971) Planetary and Space Science, Vol. 19, p.749. See also: Ishiguro, S.; Kamimura, T.; Sato, T., "Double layer formation caused by contact between different temperature plasmas" (1985) Physics of Fluids (ISSN 0031-9171), vol. 28, July 1985, p. 2100-2105.
    Torven, S. ""Formation of Double Layers in Laboratory Plasmas (1976) Astrophysics and Space Science Library, Vol. 74, p.109
    Stenzel, R. L., "Double layer formation during current sheet disruptions in a reconnection experiment" (1982) Geophysical Research Letters, vol. 9, June 1982, p. 680-683.
    Thiemann, H.; Singh, N.; Schunk, R. W. "Formation of v-shaped potentials" (1983) In ESA Sixth ESA Symp. on European Rocket and Balloon Programs and Related Res. p 269-275
    Yamamoto, Takashi; Kan, J. R. "Double layer formation due to current injection" (1985) Planetary and Space Science, Volume 33, Issue 7, p. 853-861.
    Williams, A. C. et al "Accretion onto neutron stars with the presence of a double layer" FULL TEXT (1986) Astrophysical Journal, Part 1 (ISSN 0004-637X), vol. 305, June 15, 1986, p. 759-766. PEER REVIEWED
    Peratt, Anthony L. "Evolution of the plasma universe. I - Double radio galaxies, quasars, and extragalactic jets" (1986) IEEE Transactions on Plasma Science (ISSN 0093-3813), vol. PS-14, Dec. 1986, p. 639-660. Full text: (Part I | Part II ]) FULL TEXT PDF
    Lennartsson, W. "Some Aspects of Double Layer Formation in a Plasma Constrained by a Magnetic Mirror" (1987) NASA Conference Publication, #2469. Washington, DC: NASA Scientific and Technical Information Branch., p.275 (Record | Full text) FULL TEXT
    Lindberg, Lennart "Observations of propagating double layers in a high current discharge" FULL TEXT (1988) Astrophysics and Space Science (ISSN 0004-640X), vol. 144, no. 1-2, May 1988, p. 3-13. PEER REVIEWED
    Raadu, Michael A.; Rasmussen, J. Juul "Dynamical aspects of electrostatic double layers" FULL TEXT (1988) Astrophysics and Space Science (ISSN 0004-640X), vol. 144, no. 1-2, May 1988, p. 43-71 PEER REVIEWED
    Singh, Nagendra; Hwang, K. S. "Electric potential structures and propagation of electron beams injected from a spacecraft into a plasma" (1988) Journal of Geophysical Research (ISSN 0148-0227), vol. 93, Sept. 1, 1988, p. 10035-10040.
    Lembege, B.; Dawson, J. M. "Formation of double layers within an oblique collisionless shock" (1989) Physical Review Letters (ISSN 0031-9007), vol. 62, June 5, 1989, p. 2683-2686
    Bulgakova, Nadezhda M. et al "Double layer effects in laser-ablation plasma plumes" (2000) Physical Review E (Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics), Volume 62, Issue 4, October 2000, pp.5624-5635
    Singh, Nagendra "Spontaneous formation of current-driven double layers in density depletions and its relevance to solitary Alfven waves" (2002) Geophysical Research Letters, Volume 29, Issue 7, pp. 51
    Halekas, J. S.; Lin, R. P.; Mitchell, D. L. "Inferring the scale height of the lunar nightside double layer" (2003) Geophysical Research Letters, Volume 30, Issue 21, pp. PLA 1-1
    Block, L. P. "A double layer review" FULL TEXT (1978) Astrophysics and Space Science, vol. 55, no. 1, May 1978, p. 60. {[peer}}
    Hasan, S. S.; Ter Haar, D. "The Alfven-Carlquist double-layer theory of solar flares" FULL TEXT (1978) Astrophysics and Space Science, vol. 56, no. 1, June 1978, p. 92. PEER REVIEWED
    Block, L. P. "A double layer review" {[full}} (1978) Astrophysics and Space Science, vol. 55, no. 1, May 1978, p. 65. PEER REVIEWED
    Peratt, Anthony L. Physics of the Plasma Universe (1992) Springer-Verlag
    Torven, S. "High-voltage double layers in a magnetised plasma column" (1982) Journal of Physics D: Applied Physics, Volume 15, Issue 10, pp. 1943-1949
    B Song, N D Angelo and R L Merlino "Stability of a spherical double layer produced through ionization" (1992) ournal of Physics D: Applied Physics, Volume 25, Issue 6, pp. 938-941
    Koenraad Mouthaan and Charles Süsskind, Statistical Theory of Electron Transport in the Smooth-Bore Magnetron (1966) Journal of Applied Physics June 1966, Volume 37, Issue 7, pp. 2598-2606
    Carlqvist, P. "On the physics of relativistic double layers" FULL TEXT (1982) Astrophysics and Space Science, vol. 87, no. 1-2, Oct. 1982, p. 21-39 PEER REVIEWED
    Hamilton, R. J., Lamb, F. K., & Miller, M. C. "Disk-accreting magnetic neutron stars as high-energy particle accelerators" FULL TEXT (1994) (p.939) Astrophysical Journal Supplement Series (ISSN 0067-0049), vol. 90, no. 2, p. 837-839
    Alfven, H. "Paradigm transition in cosmic plasma physics" (1982) Physica Scripta, vol. T2:1, 1982, p. 10-19
    Alfven, H.; Carlqvist, P. "Interstellar clouds and the formation of stars" FULL TEXT (1978) Astrophysics and Space Science, vol. 55, no. 2, May 1978, p. 487-509 PEER REVIEWED
    S Torven, L Lindberg and R T Carpenter "Spontaneous transfer of magnetically stored energy to kinetic energy by electric double layers" (1985) Plasma Phys. Control. Fusion 27 143-158
    Raadu, Michael A.; Rasmussen, J. Juul "Dynamical aspects of electrostatic double layers" FULL TEXT (1988) Astrophysics and Space Science (ISSN 0004-640X), vol. 144, no. 1-2, May 1988, p. 43-71. PEER REVIEWED
    Gimmell, Jennifer et al "Bio-plasma physics: Measuring Ion Transport Across Cell membranes with Plasmas" (2002) American Physical Society, Ohio Section Fall Meeting in conjunction with, abstract #1P.017
    Mituo Uehara et al "Physics and Biology: Bio-plasma physics" American Journal of Physics May 2000 Volume 68, Issue 5, pp. 450-455
    Alfven, H. "Cosmology in the plasma universe - an introductory exposition" IEEE Transactions on Plasma Science (ISSN 0093-3813), vol. 18, Feb. 1990, p. 5-10.
    G. L. Rogoff, Ed., "Introduction", IEEE Transactions on Plasma Science, vol. 19, p. 989, Dec. 1991. See extract on the Plasma Coalition web site
    Langmuir, Irving "The Interaction of Electron and Positive Ion Space Charges in Cathode Sheaths" (1929) Physical Review, vol. 33, Issue 6, pp. 954-989
    Alfvén, H., "On the theory of magnetic storms and aurorae", Tellus, 10, 104,. 1958.
    Mozer, F. S. "Observations of paired electrostatic shocks in the polar magnetosphere" (1977) Physical Review Letters, vol. 38, Feb. 7, 1977, p. 292-295
    Bostrom, Rolf "Observations of weak double layers on auroral field lines" (1992) IEEE Transactions on Plasma Science (ISSN 0093-3813), vol. 20, no. 6, p. 756-763
    Torven, S.; Lindberg, L. "Properties of a fluctuating double layer in a magnetized plasma column" (1982) Journal of Physics D: Applied Physics, Volume 13, Issue 12, pp. 2285-2300
    Volwerk, M. "Radiation from electrostatic double layers in laboratory plasmas" (1993) Journal of Physics D: Applied Physics, Volume 26, Issue 8, pp. 1192-1202
    Hasan, S. S.; Ter Haar, D. "The Alfven-Carlquist double-layer theory of solar flares" FULL TEXT (1978) Astrophysics and Space Science vol. 56, no. 1, June 1978, p. 89-107 PEER REVIEWED
    Khan, J. I. "A model for solar flares invoking weak double layers" FULL TEXT (1989) Astronomical Society of Australia, Proceedings (ISSN 0066-9997), vol. 8, no. 1, 1989, p. 29-31 PEER REVIEWED
    Volwerk, Martin; Kuijpers, Jan "Strong double layers, existence criteria, and annihilation: an application to solar flares" (1994) Astrophysical Journal Supplement Series (ISSN 0067-0049), vol. 90, no. 2, p. 589-593

Külső hivatkozások

    A double layer review (1978), L.P. Block
    Electrostatic double layers and a plasma evacuation process (1981), Raadu, M. A.; Carlqvist, P.
    On the physics of relativistic double layers (1982), Per Carlqvist
    On the role of double layers in astrophysical plasmas (1985), Smith, R. A.
    Double Layers in Astrophysics (1987) Proceedings of Workshop held in Huntsville, Ala., 17-19 Mar. 1986 sponsored by NASA, Washington and USRA. (Contents) (NASA Record) Full text PDF
    Dynamical aspects of electrostatic double layers (1988) M. A. Raadu, & J. J. Rasmussen
    Filamentary Double Layers (PDF, 1993), W.L. Theisen, R.T.Carpenter, R.L.Merlino
    Energy release in double layers (1985), Raadu, M. A.
    Parallel electric fields accelerating ions and electrons in the same direction (1988), Hultqvist, Bengt; Lundin, Rickard
    Parallel electric fields in the upward current region of the aurora: Numerical solutions (2002, PDF), R.W. Ergun, et al.
    Numerical modeling of low-pressure plasmas: applications to electric double layers (2006, PDF), A. Meige, PhD thesis

Referenciák

    Alfvén, H., On the theory of magnetic storms and aurorae, Tellus, 10, 104,. 1958.
    Peratt, A., Physics of the Plasma Universe, 1991
    Raadu, M.,A., The physics of double layers and their role in astrophysics, Physics Reports, 178, 25 - 97, 1989.