Kézikönyv - 01. fejezet - Távolságok az űrben
Bob Johnson, Jim Johnson - 2011. szeptember 2.
1.1 A csillagok távolsága
Ha felnézünk az éjszakai égre rengeteg csillagot látunk. Sok közülük olyan, mint a mi Napunk. Úgy tűnik, nagyon közel helyezkednek el, de valójában messze vannak egymástól. A távolság hatalmas közöttük.
A távolság fontos és nehezen meghatározható mennyiség a csillagászatban. Fontos tudnunk, hogy milyen közel vagyunk a csillagokhoz és galaxisokhoz, mert sok minden függ közvetlenül ettől az adattól - a kibocsátott teljes energia (abszolút fényesség), tömegek az orbitális pályán, csillagok "igazi" mozgása az űrben és a valódi fizikai méretek.

A csillagok olyan messze vannak, hogy még a távcsövön keresztül is csak apró fénypontoknak látszanak. A távolság ismerete nélkül nem lehet pontosan meghatározni, hogy egy távoli, nagyon fényes vagy egy nagyobb, de kevésbé fényes, közeli csillagot látunk-e. Ez igaz a galaxisok, kvazárok, jet-ek és egyéb távoli jelenségek vizsgálatakor is.
A két szemünk közötti távolság biztosítja számunkra a mélység érzékelését. A szemeinket bizonyos szögben kell tartanunk a tárgy érzékelésekor. Az agy ezeknek a szögeknek a segítségével beállítja a szem fókuszát, megadja a távolságérzetet és kialakítja a körülvevő világ mélységi képét. Ennek a biológiai szögeltérés észlelésének képessége jelenti a csillagászati parallaxis számítás alapját.
A háromszögelés vagy trigonometriai parallaxis közvetlen módon használja fel az objektum két pozícióban mért szögének különbségét. Azáltal, hogy megmérjük a vizsgált csillag pozícióját a nagyon távoli háttér csillagokhoz képest, majd 6 hónappal később, a Föld Nap körüli pályájának túloldalán megismételjük a mérést, meg tudjuk határozni a vizsgált csillag távolságát.
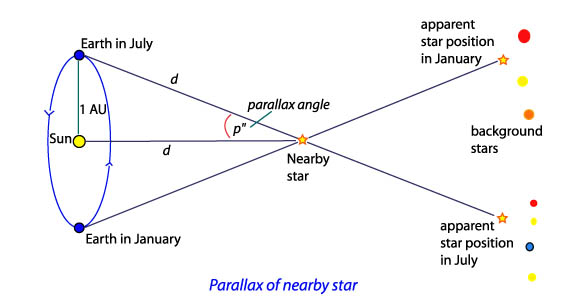
A Föld átlagosan 149.6 millió kilométer távolságra kering a Nap körül, ez a közel kör alakú pálya sugara. Ezt a távolságot gyakran Csillagászati egységnek (CsE, angolul AU) nevezzük. Így a Föld pályájának két átellenes pontja hozzávetőlegesen 2 CsE távolság, azaz 299 millió km. Amikor megmérjük a legközelebbi csillag (Alpha Centauri) irányszögét, majd 6 hónap múlva megismételjük a mérést, nagyon kis különbséget kapunk. A mérés hihetetlenül nagy pontosságot igényel.
A csillagászati parallaxis mérésről itt és itt olvashat angolul, itt és itt pedig magyarul.
Az Európai Űrügynökség (ESA) Hipparcos automatizált műholdas teleszkópja, több mint 118.000 csillag távolságát mérte meg az élettartama során - 1989-1993 között. Küldetés: a katalogizált csillagok távolságadataink pontosítása, a Tycho és a Tycho 2 katalógus frissítése. Az újonnan mért parallaxis adatok 20.870 csillag esetében feleltek meg a 10% vagy 10% alatti parallaxis hiba kritériumának.
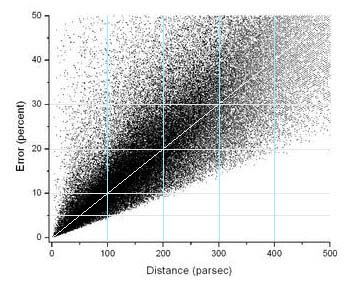
Még a pontosabb Hipparcos műholdas adatokat nézve is, a 10 százalékos hibahatáron belül hozzávetőlegesen 200-220 fényév távolságig mérhetünk, 500 fényév távolság felett a mérés egyre pontatlanabb, a trigonometrikus távolságmérés már nem használható. Richard Pogge szerint a Hipparcos adatok "1000 fényéven belül adnak jó távolság adatokat", de a becsült távolság mindössze 500 fényévig, ± 20% -30% hiba határig értékelhető, e távolság felett már sok haszna nincs. 1000 fényév szinte felfoghatatlan távolság, mégis csak mintegy 1%-a az egész Tejútrendszernek.
Egy ív fok 60 szögpercre osztható fel (60'), mint ahogy az órát 60 percre oszthatjuk. Hasonlóképpen egy ív szögpercet 60 szögmásodpercre (60") oszthatunk. Minden csillag parallaxisa, a Napot kivéve, kevesebb, mint egy ív másodperc. Az Alpha Centauri parallaxisa körülbelül 0,75 ív másodperc, vagyis 0,0002 fok. A parallaxisszög minden más csillag esetén még kevesebb, mint ez a kis érték.
Egy fényév az a távolság, amelyet a fény a vákuumban egy év alatt megtesz, hozzávetőlegesen tízbillió km azaz 9.460.528.400.000 km. Egy csillag parallaxisát ív másodpercben kifejezve elosztjuk 3,26-tal, megkapjuk a csillag távolságát fényévben. A csillagászok általában inkább parszek-ben (pc) (parallaxis secundum) és nem fényévben mérik a távolságot, habár a parallaxis méréseket csak a Naphoz viszonylag kis távolságra lehet pontosan használni.
Példa: (3,26 / 0,75 ívmásodperc) = 4,36 fényév, azaz 41.25 billió km vagy 1,33 parszek távolság a legközelebbi csillagig.
Kezdjük hozzánk közelebb.
1.2 Távolságok modellezése a Naprendszerben és környékén
Robert Burnham kidolgozott egy modellt, amely hétköznapi kifejezésekkel modellezi, hogy mennyi hely van a csillagok környezetében. Ahhoz, hogy megértsük a skálát, tudnunk kell néhány valódi távolságot.
Fentebb írtuk, hogy a Nap-Föld távolság hozzávetőlegesen 149,605,000 km. Általában kerekítjük 150 millió km-re és 1 Csillagászati egységnek (CsE) hívjuk.
Egy fényév 63.294 CsE. Ez véletlenül körülbelül ugyanannyi, mint a ahány hüvelyk (2,54cm) van (63.360 db) egy angol mérföldben (1,61km). Tehát, körülbelül azonos számú hüvelyk található egy Csillagászati egységben (63.360 x 92.960.000), mint ahány mérföld egy fényévben (63.294 x 92.960.000). Ezek igazán nagy számok! Folytassuk a számolást hüvelykben.
Burnham úgy skálázta a modelljét, hogy 1 hüvelyk (1") értéke 1 CsE vagy 93 millió mérföld. Így 1 angol mérföld a modellben egyenlő 1 fényévvel. A skála így 1: 6.000.000.000.000. Egy egység hat millió millió valós egységet képvisel, vagyis egy a 6 trillióhoz, 1: 6 × 10¹².
Kezdjük a Naprendszerünk leírását Burnham miniatűr makettjével. Tudjuk, hogy a távolság a Föld és a Nap között (1 CsE) lesz egy hüvelyk. Mekkora lesz a Nap? A Nap átmérője körülbelül 870.000 mérföld, így a mi méretarányos modellünkben a Nap egy kicsit kevesebb lesz, mint 1/100 hüvelyk (0,254mm) átmérőjű. Ez egy nagyon pici porszem. A Föld egy hüvelykre található a Naptól, de olyan kicsi a mérete (0,00009" vagy 0,002286mm), hogy nem lennénk képesek mikroszkóp nélkül megfigyelni.

A Plútó keringési sugara 39,5-szer nagyobb, mint a Földdé, így a Plútó 39,5 hüvelyk, vagyis majdnem pontosan 1 méter távolságra kering a Naptól.
A helioszféra, a Nap körüli régió, ameddig a napszél eljut, körülbelül 7 láb (2,13m) távolságra adódik.
Szóval hol is van a legközelebbi csillag a modellben? A legközelebbi szomszéd Alpha Centauri, amely több mint 4 fényévre található, a modellben több, mint 4 mérföldre (~6.5km) kerül.
Igen, 6 és fél km. Modellünkben a Nap egy apró pötty és 6 kilométerre található a legközelebbi porszemhez. Rengeteg üres hely van közöttük. Tehát mekkora lesz mi galaxisunk ebben az apró modellben? A galaxisunk modellje hozzávetőlegesen 161.000 km széles lenne. A spirálkarok 1600 km vastagok és a csillagokból álló központi dudor magassága 10.000 km lenne. A mi galaxisunk csak egy a több száz milliárd látható galaxis közül, amelyet megfigyelhetünk a jelenlegi eszközeinkkel az Univerzumban. Az éjszakai égbolt látszólag csillagokkal zsúfolt, de a csillagok egymástól jellemzően az átmérőjük több mint 10 milliószorosával messzebb vannak egymástól.
1.3 Távolság és gravitáció
Emlékezzünk arra, hogy mit is írt Newton: a gravitációs erő csökken (azaz fordítottan arányos) a két objektum közötti távolság négyzetével. Vagyis a gravitációs vonzás két, 6 km távolságra lévő pötty között nem valami erős, akárcsak két, 4 fényévnyire eső csillag között sem. Nézzük, hogyan használhatjuk Newton egyenleteit valójában!
Az alábbi egyszerű egyenletben F az erő (Newton), G egy nagyon kis számú, úgynevezett gravitációs állandó, M1 és M2 a két csillag becsült tömege kg-ban és r a csillagok középpontjai között mérhető távolság. A csillagászok metrikus (SI) mértékegységrendszert használnak, mert jóval elterjedtebb és sokkal kényelmesebb, mint a hagyományos angolszász imperial rendszer (hüvelyk, láb, mérföld, font és uncia). A számítás eredménye az alábbi táblázatban látható. A gravitációs gyorsulás (g) behelyettesítése a Föld felszínén mérhető gravitációs erő felhasználásával történt.
F = G × (M1 × M2) ÷ r²
Mértékegységek méter, kg, másodperc:
| Nap és Centaurus A+B távolsága d= | 4,395 | Fényév | 9.4608E+15 m/fényév |
| -""- | 41.580.216.000.000.000 | m | |
| M1, Nap tömege, kg | 1,99E+30 | kg | |
| M2, Centaurus A+B, kg | 3,88E+30 | kg | |
| Gravitációs állandó (G) | 6,67428E-11 | ||
| Tömegek szorzata, M1*M2 | 7,72E+60 | kg2 | |
| Távolság négyzete, d2 | 1,73E+33 | m2 | |
| F=G*(M1*M2) / d2 | Gravitációs erő két tömeg között | d=két tömeg távolsága | |
| A Napra ható erő, F= | 2,98E+17 | Newton | |
| g=9,8m/s2 | gravitációs gyorsulás a Földön | ||
| F=m*a | |||
| Átalakítva: a = F/m | 1,50E-13 | m/s2 | |
| elosztva 9,8-al, a g: | 1,528E-14 | A földi "g"a Nap középpontjában | |
| Az Centaurus A+B Napra ható gravitációs ereje, számítás | |||
A nagy tömeg ellenére a két csillag minimális gravitációs gyorsulást gyakorol egymásra. Bármilyen erő is legyen felelős a Világegyetemben az anyag viselkedéséért, elég erősnek és hatékonynak kell lennie az óriási távolságok miatt.
Newton gravitációs törvénye elég jól elmagyarázza a vonzó- és orbitális mozgásokat a Naprendszer korlátozott területén. De a viszonylag gyenge gravitációs erő csak akkor működhet hatékonyan nagy csillagközi távolságokon keresztül, ha a tér üres és nincsenek más versengő erők, amelyek felülbírálják a gravitációt.
Vége az 1. fejezetnek
