Kézikönyv - 02. fejezet - Mágneses és elektromos erők az űrben
Bob Johnson, Jim Johnson - 2011. október 17. (Rausch Zoltán fordítása nyomán)
2.1 A gravitációs és elektromos erők nagysága
A gravitáció meglehetősen gyenge erő. Az elektromos Coulomb-erő a proton és az elektron között 39 nagyságrenddel (1039 - 1 és 39 nulla) erősebb, mint a közöttük fellépő gravitációs erő.
| Alapvető kölcsönhatások (erők) a fizikában | ||||
|
A Wikipedia oldal alapján: Alapvető kölcsönhatások |
||||
| A kölcsönhatások (4) tulajdonságai és az azokat közvetítő bozonok áttekintő táblázata | ||||
| Kölcsönhatás | Jelenlegi elmélet | Relatív erősség | Hatótáv (m) | közvetítő |
| erős | Kvantum-színdinamika | 1.00E+39 | 1.00E-14 | gluon |
| elektromágneses | Kvantum-elektrodinamika | 1.00E+37 | végtelen | foton |
| gyenge | Elektrogyenge kölcsönhatás | 1.00E+26 | 1.00E-17 |
|
| gravitáció | Általános relativitáselmélet | 1 | végtelen | graviton1 |
|
[1] A gravitont még nem fedezték fel… A gravitációs és elektromágneses kölcsönhatás hatósugara végtelen. Az elektromágneses kölcsönhatás relatív erőssége 37 nagyságrenddel nagyobb a gravitációnál. |
||||
Ízelítőt kaphatunk az elektromágneses mezők relatív erősségéről, amikor egy kis mágnes segítségével felveszünk egy vas tárgyat, például egy csapágygolyót. Annak ellenére, hogy az egész Föld gravitációs vonzása érvényesül csapágygolyón, a mágnes könnyedén leküzdi, ha elég közel van a golyóscsapágyhoz. Az űrben a gravitáció csak akkor válik jelentős tényezővé, ha az elektromágneses erők árnyékoltak vagy semlegesíttettek.

Gömb alakú tömegek és töltések esetén, mind a nehézségi erő és az elektromos Coulomb-erő a távolság négyzetével fordítottan arányos és a távolsággal gyorsan csökken. Más geometria/térszerkezet esetén az erők távolodva kevésbé csökkenhetnek. Például az erő két, viszonylag hosszú és vékony elektromos, egymással párhuzamosan haladó vezető között fordított arányban változik az első elektromos a távolság közöttük.
Az elektromos áram képes hatalmas távolságokra energiát szállítani, mielőtt valamilyen detektálható hatást hozna létre. Hasonlóan az általunk használt elektromos energiához, amely egy távoli erőműben képződik és a konyhában működtet egy vízforralót. Ez azt jelenti, hogy nagyobb távolságra az elektromágneses erő és az elektromos áram együtt sokkal hatékonyabb, mint akár a gyenge gravitációs erő, vagy akár a sokkal erősebb elektrosztatikus Coulomb-erő.
Ne feledjük, hogy csak azért, hogy a gravitációs modellel meg tudják magyarázni az észlelési eredményeket, el kellett képzelni huszonnégyszer több anyagot, mint amennyit a Világűrben találtunk. Ráadásul ezeknek az anyagoknak különleges helyeken és speciális, láthatatlan típusúnak kell lennie. Úgy tűnik, sokkal elfogadhatóbb lenne azt megvizsgálni, hogy a fizikában jól ismert elektromágneses erők és az elektromos áram létre hozhatja -e a megfigyelt hatásokat ahelyett, olyan dolgokat találnánk ki, amelyek valószínűleg nem is léteznek.
2.2 "Vákuum" az űrben
Egészen 100 évvel ezelőttig azt gondoltuk, hogy az űr üres. A "vákuum" és az "üresség" felcserélhető. A szondák azonban azt találták, hogy az űr atomokat, port, ionokat és elektronokat tartalmaz. Habár az anyagsűrűség nagyon alacsony, de nem nulla. Ezért a Világűr nem vákuum a szó hagyományos értelmében, ahol egyáltalán nincs semmi. Például a "napszél" töltött részecskék áramlása, amely a Napból érkezik és körbeveszi a Földet. A napszél látható hatása a sarki fény.
Ismereteink szerint a porrészecskék a Világűrben 2 és 200 nanométer közötti méretűek és sok közülük elektromosan töltött. A részecskéket ionok és elektronok veszik körbe. A semleges és töltött anyag keverékét plazmának nevezzük, amelyet átjárnak az elektromágneses mezők. A 3. fejezetben foglalkozunk részletesen a plazmával és a plazma egyedülálló kölcsönhatásaival az elektromágneses mezőkkel. Az "üres" tér a bolygók, csillagok és galaxisok között nagyon különbözik attól, amit a csillagászok a 20. század első felében feltételeztek.
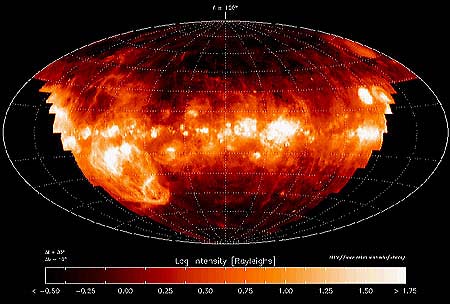
A töltött részecskék és elektromágneses mezők létezését a Világűrben a gravitációs és az elektromos modell is elfogadja. A meghatározó különbség a két modell között az, hogy mennyire veszik figyelembe a viselkedésüket. Ezért térjünk ki a mágneses mezők tulajdonságaira.

2.3 Bevezetés a mágneses mezőkbe
Mire gondolunk a „mágneses mezők” és „mágneses erővonalak” hallatán? Annak érdekében, hogy megértsük a mezők fogalmát, kezdjük egy ismerősebb példával, a gravitációval.
Azt tudjuk, hogy gravitációs erő tömeggel rendelkező testek vagy részecskék között alakul ki. Mondhatjuk, hogy a Föld gravitációja itt hat körülöttünk a felszínen és tovább terjed az űr felé. Kifejezhetjük máshogy is, a Földnek gravitációs mezeje van, mely az űr minden irányában hat. Más szóval, a gravitációs mező egy olyan régió, melyben vonzó erőt hat a tömeggel rendelkező testek között.
Hasonlóképpen a mágneses mező is egy olyan régió, melyben mágneses erő hat a mágneses vagy töltött testekre. (Látni fogjuk a későbbiekben, hogy a mágneses mezőknek mi is az eredete.) A mágneses erő hatása a legnyilvánvalóbb ferromágneses anyagok esetén. Például vasreszeléket szórva egy mágnes feletti felületre, a reszelék szemcséi a mágneses mező iránya szerint rendeződnek el, mintha kis iránytűk lennének.

A vasreszelék a déli pólustól az északi felé rendeződve koncentrikus vonalakhoz hasonló mintát hoz létre, amelyek megmutatják a mező irányát és közvetve az erősséget is az adott pontban.
A mágneses erővonalak az egyik kényelmes módja a mező irányultságának ábrázolására és támpontul szolgálnak mezőben haladó töltött részecskék útvonalának meghatározásához. (hivatkozás: Fundamentals of Plasma Physics, Cambridge University Press, 2006, Paul Bellan, Ph.D.)
Nagyon fontos megjegyezni, hogy ezek a mezővonalak fizikailag nem léteznek. Minden egyes vasreszelék darabka a mágneses mezőben úgy viselkedik, mint egy iránytű: ha elmozdítjuk egy kicsit, beáll az aktuális észak-déli irányba. Hasonlóan a függőónhoz (egy zsinór, nehezékkel a végén), mutatja egy adott helyen a gravitációs mező irányát. Hosszirányú vonalakat rajzolva a függőón mentén a gravitációs mező erővonalit kapjuk. Ezek a vonalak a valóságban nem léteznek, csupán arra valók, hogy könnyebben elképzelhessük a mező által keltett eredő erők irányát. Az „I” függelékben további részletek találhatók a témában, vagy angolul itt, a Fizzics Fizzle oldalon.
Ezek az erővonalak nem feltétlenül jelzik jól az ébredő erő irányát, bármi is hozza létre a mezőt. Az erővonalak jelezhetik az erő irányát vagy polaritását. Jelenthetik az azonos térerejű pontok határvonalát, valahogy úgy, mint ahogy a térképen a szintvonalak kötik össze az azonos tengerszint feletti magasságokat. Gyakran mágneses háromdimenziós testeknél képzeletbeli felületekkel ábrázolják az egyforma mágneses erősségű helyeket vonalak helyett.
Közmegegyezés alapján a mágneses mező iránya egy adott pontban az északi pólustól a déli felé mutat.
A gravitációs mező ábrázolásakor egy vonal az azonos gravitációs erő pontokat jelenti az irányultság helyett. Ezek a megegyező gravitációs erőt jelentő vonalak változnak a magassággal (azaz a test központjától való távolsággal), nem úgy, mint a térkép szintvonalai. Ahhoz, hogy meg tudjuk állapítani a gravitációs erő irányát egy ilyen szintvonalnál, valakinek meg kell állapítani, hogy merre mozdul el egy test az adott pontban. Egy dombra helyezett kő lefelé gurul, átszelve a szintvonalakat. Más szavakkal a gravitációs erő merőleges a mezőt jelképező vonalakra.
A mágneses mező bonyolultabb a gravitációs mezőnél, mert vonzani és taszítani is képes. Két állandó mágnes ellentétes végével (ellentétes „pólussal”, vagy É-D) szembefordítva vonzani fogja egymást a kettejük keltette kombinált mágneses mező iránya mentén (lásd fenti kép). Ellentétes polaritással szembefordítva (É-É és D-D) pedig taszítani fogják egymást ugyanabban az irányban.
A mágneses mezők erőhatást gyakorolnak a mozgó töltött részecskékre. Mivel a részecskére ható erő merőleges mind a mágneses mező, mind a töltött részecske haladási irányára, ezért a mozgó részecskének változik a haladási iránya (gyorsul) a mágneses mező hatására a mezőn áthaladva. A sebessége változatlan marad, őrizve a kinetikus energiáját. A következő képeken látszik, hogyan változik egy labor kísérlet során a vákuumban vizsgált elektron sugár útvonala a mágneses tér megjelenése előtt és után.

Második kép: Helmholtz tekercs elhelyezése a vákuumkamra körül;
Harmadik kép: Helmholtz tekercs áram alatt, a sugár elhajlása a "jobb kéz szabály szerint".
A mágneses erő hatása a töltött részecskére analóg a giroszkóp erővel. Az erővonalak „mentén” vagy azonos irányban haladó töltött részecskére nem gyakorol erőhatást a mágneses mező, amely megváltoztatná a mozgása irányát, csakúgy, mint a giroszkóp tengelye mentén ható erő sem kényszeríti azt elfordulásra vagy „kóválygásra”.
Még ha az eltérő töltésű részecskékre ható erők különbözőek, a mágneses mező erővonalakkal történő ábrázolása hasznosan szemlélteti az anyagokra, mint például a mozgó töltött részecskére ható erőt, amely kifelé mutat a mezőből.

2.4 A mágneses mezők eredete
A mágneses mező egyféle módon keletkezhet: elektromos töltésnek kell mozognia. Állandó mágneseknél a mezőt az atommag körül keringő elektronok hozzák létre. Erős mágnes akkor jön létre, ha minden atommag körül keringő elektron spinje (az elektronok spinmomentum vektora) azonos irányba mutat, erőteljes eredő mezőt alakítva ki. Az ún. Curie hőmérsékletére felmelegítve a mágnes elveszíti erejét, a hőmozgás felülmúlja a fegyelmezett forgó mozgást, ezzel nagymértékben csökkentve a létrejövő mágneses mezőt. Egy fém áramvezetőben a hosszirányban áramló elektronok hozzák létre a mágneses mezőt. Részletesebb leírás található a témáról és a ferromágnesességről itt angolul és itt magyarul.
Mozgó elektromos töltések minden esetben mágneses mezőt hoznak létre. Mozgó elektromos töltések nélkül nem jöhet létre mágneses mező. Ampère törvénye szerint a mozgó töltés által létrehozott erő körkörös és a mozgás irányára merőleges síkban van.
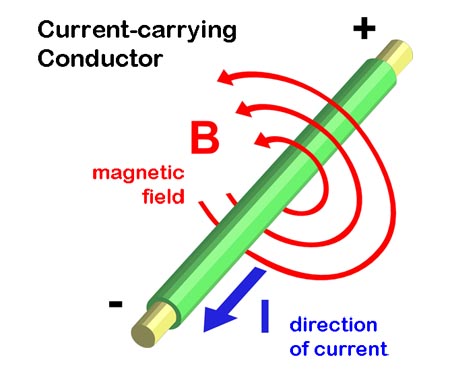
Az elektromos áramot létrehozó, láthatatlan mozgó elektromos töltéseket nehéz érzékelni, különösen nagy távolságból. Az űrben a mágneses mező észlelése (jól ismert módszer a csillagászok körében, lásd lejjebb) biztos jele a kísérő elektromos áram jelenlétének.
Ha áram folyik egy vezetőben, legyen az egy hosszú vezeték vagy egy plazma szál, akkor minden egyes töltött részecske körül egy kis mágneses mező jön létre. Ezeknek a pici, önálló mágneses mezőknek az összeadódása eredményezi a folyamatos eredő mágneses mezőt, végig a vezető körül. Az egyenlő erősségű mezők a vezetők körül (ezeket ekvipotenciális vagy “szintfelületnek” hívják) koncentrikus hengereket alkotnak.
Az időben változó elektromos és mágneses mezőre később térünk ki. (Lásd 4. fejezet és iii. függelék.)
A mágneses mező űrbeli eredetének a megválaszolása az egyik kulcsfontosságú eltérés a Gravitációs Modell és az Elektromos Modell között.
A gravitációs Modell megengedi (de nem jelezte előre – a ford.) a mágneses mezők létezését az űrben, mivel azok rendszeresen megfigyelhetők, de azt mondja, hogy azt a csillagok belsejében levő dinamó hozza létre. Ma a legtöbb kutató szerint az űrben sem elektromos tér, sem az elektromos áram nem játszik jelentős szerepet a mágneses mezők létrehozásában.
Ezzel szemben az Elektromos Modell, mint látni fogjuk részletesebben később, azt állítja, hogy az űrben is a mozgó töltött részecskék hozzák létre a mágneses teret úgy, ahogy a mágneses mező létrejön mozgó töltött részecskék körül itt a Földön. Természetesen az Elektromos Modell elfogadja, hogy a csillagoknak és bolygóknak is van mágneses terük, ezt alátámasztják magnetoszféra és más észlelések. Az új elmélet megmagyarázhatja azoknak az űrbeli mezőknek az eredetét, amelyeket a csillagok dinamóhatása nem hozhatott létre.
2.5 A mágneses mezők észlelése az űrben
Az űrkorszak kezdete óta az űrhajók fedélzeti eszközökkel képesek a Naprendszerbeli mágneses mezők mérésére. „Láthatjuk” a mágneses mezőket az űrhajók hatótávján túl, mivel a mezők hatással vannak a rajtuk áthaladó fényre és más sugárzásra. A fényre gyakorolt hatás alapján becsülhető a mágneses mező erőssége is.
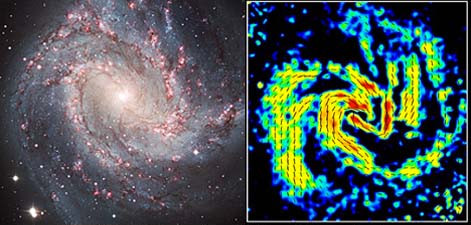
Courtesy Rainer Beck and Bill Sherwood (ret.), Max Planck Institute für Radio-Astronomie
Évszázadok óta tudunk a Föld mágneses teréről. Ma már ezeket a mezőket az űrben is tudjuk mérni és ösztönösen könnyen megérthetjük a mágneses mezők fogalmát, bár a csillagászoknak nehéz megmagyarázniuk a mezők eredetét.
A mágneses mezők sokféle hullámhosszon kimutathatók, mérve a szimmetrikus spektrográfiai emissziós vagy abszorpciós vonalak szétválását, amit a mágneses mezők okoznak. Ez Zeemann effektként vált ismertté. Pieter Zeeman (1865-1943) holland fizikus 1902-ben kapott érte Nobel díjat. Figyeljük meg a fenti képen az M83 galaxis jobb oldali mágneses vonalai mennyire igazodnak a bal oldali képen látható galaktikus karokhoz.

A mágneses mező jelenlétére utaló másik jel, a mágneses mező hatására az elektronok által kibocsátott szinkrotron sugárzás polarizációja, amely galaktikus skálán hasznos. Érdemes megnézni Beck angol nyelvű cikkét a Galaktikus mágneses mezőkről a Scholarpedia oldalon, továbbá Beck és Sherwood közeli galaxisok mágneses mezőiről készített atlaszát. A polarizáció mértékét a Faraday-effektus segítségével mérték. A Faraday-rotáció mértékéből származtatható annak a mágneses mezőnek az erőssége, amelyen polarizált fény keresztülhalad.
Philipp Kronberg angol nyelvű oktatási anyaga a „Measurement of the Electric Current in a Kpc-Scale Jet” (Az elektromos áramerősség mérése Kiloparszek hosszú jet-ekben) lenyűgöző betekintést nyújt a hatalmas galaktikus kilövellésben található erős „csomók” mérhető Faraday fordítása, az eredő mágneses mező erőssége valamint a jelen levő kilövellés elektromos áramának közvetlen kapcsolatáról.
A mágneses mezőket az Unvierzum Gravitációs Modellje és az Elektromos Modell is tartalmazza. Az alapvető különbség közöttük, hogy az Elektromos Modell felismeri a mágneses mezőket mindig kísérő elektoros áramokat is. Most az elektromos mezők és áramok következnek.
2.6 Bevezetés az elektromos mezőkbe
Az elektromos töltésnek polaritása van, ami lehet negatív és pozitív. Megegyezés szerint a töltés elemi (legkisebb) egysége egyenlő egy elektron (-e) vagy proton (+e) töltésével. Az elektromos töltés kvantált, mindig az (e) többszöröse.
Az alapegység a coulomb (C), ahol e = 1.6×10-19 coulomb. Ha megfordítjuk az egyenlet, egy coulomb a 6.25×1018 egyszeres töltés részecskét jelent. Egy amper (A) egy coulomb per másodpercet jelent. A 20A esetén 20C töltés per másodperc, vagyis 1.25×1020 elektron per másodperc sebességgel halad el az áram egy adott fix pont mellett.
Minden töltéshez elektromos mező társul. Az elektromos mező abban hasonlít a mágneses mezőhöz, hogy az alapvető erő, az elektromágneses kölcsönhatás hozza létre és a "hatósugara” vagy a hatás mértéke végtelen, vagyis a végtelenül nagy. Egy egyszerű töltött részecskét gömb alakú elektromos mező vesz körül, hasonlóképpen, mint a gravitációs mező egy kis tömegpont vagy egy nagy gömbszerű anyagot.
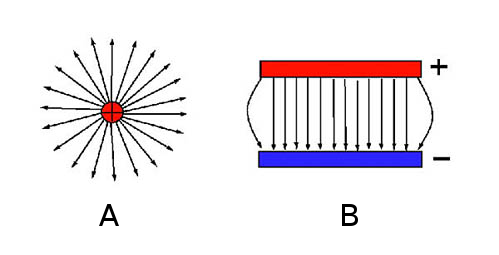
Adott pontban az elektromos mező erősségét newtonban (N) meghatározzuk meg, az az erőhatás, amelyet egy pozitív 1 coulomb töltésű próbatestre hat. Mint a gravitáció, a töltésre ható erő is fordítottan arányos a távolság négyzetével egy próba (vagy bármilyen más) töltés esetén.
Egy adott pontban egy pozitív teszt töltés következetesen meghatározza az erő irányát, ami hatni fog egy másik töltésre. Azonos töltések taszítják egymást, a különbözőek vonzzák, hasonlóan a mágneses pólusokhoz. A képzeletbeli elektromos mező vonalak a pozitív töltéstől a negatív töltés felé mutatnak. Nézd meg a következő kis angol nyelvű YouToube videót ez elektromos mezőről itt.
Itt találsz egy felhasználó által irányított elektromos mező bemutató Mathematica alkalmazást két töltéssel és a hozzájuk kapcsolódó erővonalakról.
Lehet, hogy szükség lesz egy Mathematika vagy CDF lejátszó letöltésére (csak egyszer kell letölteni és ingyenes) a belinkelt oldalról a demó lejátszásához. Beállíthatjuk a töltés polaritását (+ vagy -) és erősségét a csúszkákkal. Mozgatni is lehet a töltött részecskéket a képernyőn. Időt kell hagyni a mező vonalak finom rendeződéséhez a változtatások között.
Az űrbeli plazmáiban az elektromágneses erők általában erősebbek, mint a gravitációs erők. Az elektromágnesességet lehet árnyékolni, nem úgy, mint a gravitációt, legalábbis ma így tudjuk. Az általános érvelés a Sztenderd Modellben hogy a legtöbb elektron egy adott területen vagy testben protonokkal párban található az atomok és molekulák magjában, így a pozitív és negatív töltések oly tökéletesen kioltják egymást, hogy „nagy testek esetén a gravitáció a meghatározó” (Link: alapvető kölcsönhatások, lásd az Elektromágnesesség alcím alatt).
Azt hagytuk figyelmen kívül fentiekben, hogy a relatíve hideg, stabil és közel semleges bolygók környezete - mint itt a Földön is – a ritka kivételek közé tartozik. A legtöbb anyag a Világegyetemben plazmából áll, vagyis töltött és semleges részecskék mozognak a töltés elkülönülés komplex szimfóniájára az elektromos és mágneses mezők saját törvényei szerint. Gravitáció, habár mindig jelen van, általában nem a domináns erő.
Messze a főként semlegesített töltésektől és a gyenge mágneses és elektromos mezőkből álló és hozzájuk kapcsolódó gyenge áramoktól, az űrplazmában az elektromos terek és áramok gyakran nagyon nagyok és erősek lehetnek. Az Elektromos Modell tartalmazza az olyan jelenségeket, mint a magnetoszférák, Birkeland áramok, csillagok, pulzárok, galaxisok, galaxis és csillag jet-ek, planetáris csillagködök, "fekete lyukak", olyan energikus részecskék, mint a gamma-sugárzás, a Röntgen sugarak a plazmafizika alapvető elektromos eseményei. Még a sziklás testek - bolygók, kisbolygók, holdak és üstökösök, valamint a gáz-testek a csillagok hélioszférájában sem mentesek az elektromágneses erőktől és azok hatásaitól.
Minden különálló elektromosan töltött részecske hozzájárul az elektromos mező egészéhez. A komplex elektromágneses mező nettó ereje egy tetszőleges pontban vektorokkal számolható, ha a töltésekről feltételezhető hogy állnak. Ha töltések mozognak (és mindig azt teszik), akkor létrehoznak – egymásra hatva – mágneses mezőket, ami megváltoztatja a mágneses elrendeződést is. A mágneses mező változása változtatja az elektromos mezőket és ez visszahat az áramokra, így a mezők, amik a mozgó részecskékből jönnek létre nagyon komplex kölcsönhatásokat mutatnak folytonos visszacsatolásokkal és bonyolult matematikával.
A töltések az űrben bármilyen térbeli elrendeződést felvehetnek. Amennyiben a töltések pontszerű vagy gömbszerű elrendeződés helyett egy egyenes mentén oszlanak szét, és a töltött részecskék hossza sokkal nagyobb, mint a szélessége vagy átmérője, akkor a vezetőt körülvevő elektromos mező hosszúkás henger alakú és azonos erőpotenciálú koncentrikus részekből áll. Az ilyen mezők erőssége a formációktól távolodva lineárisan csökken, azaz a központi tengelytől való távolsággal fordítottan (és nem a távolság négyzetével) arányosan csökken. Ez nagyon fontos az űrbeli mágneses mezők sodronyszerű áramainak tanulmányozásakor, mint pl. a villámcsapás, koncentrált plazma fókusz vagy a hatalmas Birkeland áramok.
Ne felejtsük el, hogy a pozitív töltésre ható erő a pozitív töltéstől indul a negatív felé, vagy negatív töltés hiányában a végtelenbe vész. Már egy kis töltéskülönbség esetén is, mondjuk, kicsit több pozitív töltésű részecske itt és több negatív töltésű részecske messzebb, elég ahhoz, hogy a két területrész között erő ébredjen, a különböző töltésű elválasztott részek között elektromos mező alakuljon ki. Az elrendezés kiemelt fontossága világosabbá válik a plazma kettősréteg későbbi tárgyalásakor.
Gondoljunk egy elektromos kondenzátorra, ahol két elválasztott lemez vagy felület (fegyverzet) helyezkedik egymással szemben, hasonlóan a korábbi „B” ábrán levő lemezekhez. Elektromos mező alakul ki a lemezek között. Bármely ott mozgó vagy odahelyezett töltés gyorsulni kezd az ellentétes töltésű felület felé. Az elektronok (melyek töltése negatív) gyorsulnak a pozitív felület felé, míg a pozitív ionok és protonok a negatív felület irányába.

Newton törvényei szerint az erő gyorsulást eredményez. Így az elektromos mező hatására a töltött részecskék sebességre tesznek szert. Az ellentétesen töltött részecskék az ellentétes irányba fognak mozogni. Az elektromos áram a definíció szerint a töltés mozgása egy ponthoz képest. Így az elektromos mezők elektromos áramot hoznak létre azáltal, hogy sebességet adnak a töltött részecskéknek.
Ha egy elektromos mező eléggé erős, akkor a töltött részecskék nagyon nagy sebességre gyorsulnak a mező által. Továbbiakat az elektromos mezőkről itt találsz angolul.
2.7 Az elektromos mezők és áramok érzékelése az űrben
Az elektromos mezők és áramok érzékelése sokkal körülményesebb, ha nem helyezhető a mezőbe közvetlenül a mérőeszköz, ám megmérhetjük az áramokat a Naprendszerben űrhajó segítségével. Az elsők között az alacsony sarki pályán keringő TRIAD műhold volt az 1970-es években, mely elektromos áramot érzékelt a Föld felső légkörében. 1981-ben Hannes Alfvén írta le a helioszférikus áram modellt a Cosmic Plasma című könyvében.
Azóta, azt az elektromos áram járta felszínt, mely elválasztja a Nap pozitív és negatív mágneses térségeit egymástól, Hélioszférikus Áram Lepelnek (HCS - heliospheric current sheet) hívják. Ez kb. 15 fokkal tér el a Naprendszer síkjától. Körülbelül a napciklus feléig a kifelé mutató mágneses mezők vannak a HCS felett és a befelé mutatóak alatta. A napciklus második felénél megfordul, amint a Nap mágneses polaritást vált. Ahogy a Nap forog, a HCS forgása „elteríti” a hullámokat, ezt a NASA terminológia „sztenderd Parker spirálnak” hívja.
Néhány link, mely a HCS-t bemutatja angolul: Wikipedia, NASA, this Mathematica demonstration, and the Belgian Institute of Aeronomy.
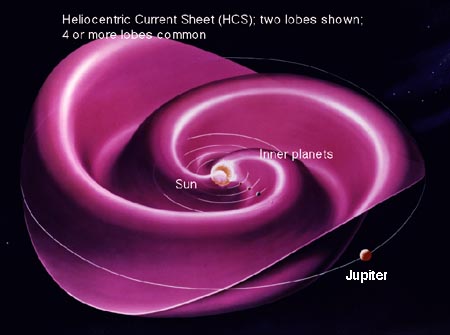
1980 óta különböző helyeken mérték meg űrhajók a HCS változását. Érzékelték mind a földközeli mind a nap-áramokat. A Gravitációs Modell elfogadja, hogy ezek az áramok az űrben léteznek, de feltételezi, hogy a mágneses mezők hozzák létre. Erre még visszatérünk.

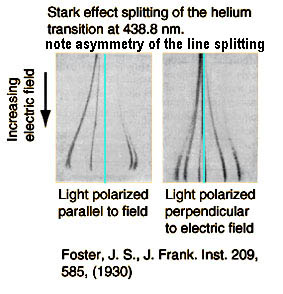
Az űrhajók hatósugarán kívül eső elektromos mezők nem detektálhatók olyan pontossággal, mint a mágneses mezők. A spektrográfiai vonalak felhasadása vagy szélesedése bekövetkezik, ha a fény elektromos mezőn halad át, de a mágneses mező szimmetrikus vonalaival ellentétben a kapott vonalak aszimmetrikusak. További különbség, hogy az elektromos mező vonal szélesedése a kibocsátó anyag tömegére utal (a könnyebb elemek szélesebb rést, nehezebbek keskenyebbet okoznak), amíg a Zeeman (mágneses mező) szélesedése független a kibocsátó anyag tömegétől. Az aszimmetrikus spektrográfiai vonalhasadást az ún. Stark hatást, Johannes Starkról (1874-1957) nevezték el.
Egy másik módja annak, hogy következtetni tudunk az elektromos mezők jelenlétére, a töltött részecskék viselkedésének hatásain alapul. Főleg azoknak a részecskéknek a hatásain, amelyek nagy sebességre felgyorsultak fel. Ezek a töltött részecskék elektromágneses sugárzást, pl. Röntgen sugarakat bocsátanak ki, amelyet már régóta ismerünk és a Földhöz-kötött tapasztalataink szerint erős elektromos mezővel generálunk.
Az elektromos áramok űrbeli alacsony sűrűségű plazmában úgy viselkednek, mint a vákuumos üveg vagy Crooks csövekben fluoreszkáló fények. Gyenge áram esetén a plazma sötét és nagyon kevés látható fényt bocsát ki (ellenben a hideg, gyenge plazma sokat sugároz rádió és infravörös hullámtartományban). Ahogy az áram növekszik, a plazma átvált izzásba, mérsékelt elektromágneses sugárzást kibocsátva a látható spektrumban. Ez látható a fejezet végén levő képen. Ha az átfolyó elektromos áram nagyon naggyá válik, plazma ív alakul ki. Bár más a lépték, de kicsi a különbség a villámlás és egy csillag fotoszférájának a sugárzó felszíne között.
Természetesen többféle magyarázat is létezhet mindezekre a jelenségekre, legalábbis elméletben. A Gravitációs Modell feltételezi, hogy a gyenge gravitációs kölcsönhatás természetfeletti sűrűség által megsokszorozódik, az így létrejövő fekete lyukak vagy neutron csillagok hozhatják létre ezeket a jelenségeket. Vagy éppen szupernóva robbanás során közel a fénysebességre gyorsuló részecskék. A kérdés az, hogy a „megsokszorozott gravitáció” vagy laborban tesztelhető elektromágnesesség áll közelebb ahhoz a megfigyeléshez, hogy a Világegyetem plazmából áll.
Az elektromos modell szerint az elektromos jelenségek nem csak a Naprendszer űrhajók által elérhető részeire korlátozódnak. Az Elektromos Modell feltételezi, hogy hasonló elektromos jelenségek zajlanak a Naprendszeren túl is. Végtére is, nem lenne furcsa, ha a Naprendszer volna az egyetlen hely a világon, ahol elektromos jelenségek fordulnak elő az űrben?

Kép: T.A. Rector, University of Alaska, Anchorage, and Kitt Peak WIYN 0.9m telescope/NOAO/AURA/NSF
Vége a 2. fejezetnek
